MATTopo: Topology-preserving Medial Axis Transform with Restricted Power Diagram

accepted to ACM Transactions on Graphics (SIGGRAPH Asia 2024)

Ningna Wang, University of Texas at Dallas
Hui Huang, Shenzhen University
Shibo Song, Independent Researcher
Bin Wang, Tsinghua University
Wenping Wang, Texas A&M University
Xiaohu Guo, University of Texas at Dallas
ArXiv (low res) Supplement (pdf) Code Video (8min)

A gallery of our topology-preserving 3D medial axis results. The input shapes are shown in transparency, while the computed medial axis are shown in blue (left) and brown (right) colors. The left side displays the medial axis computed on CAD models, and the right side shows those on organic models.

Abstract

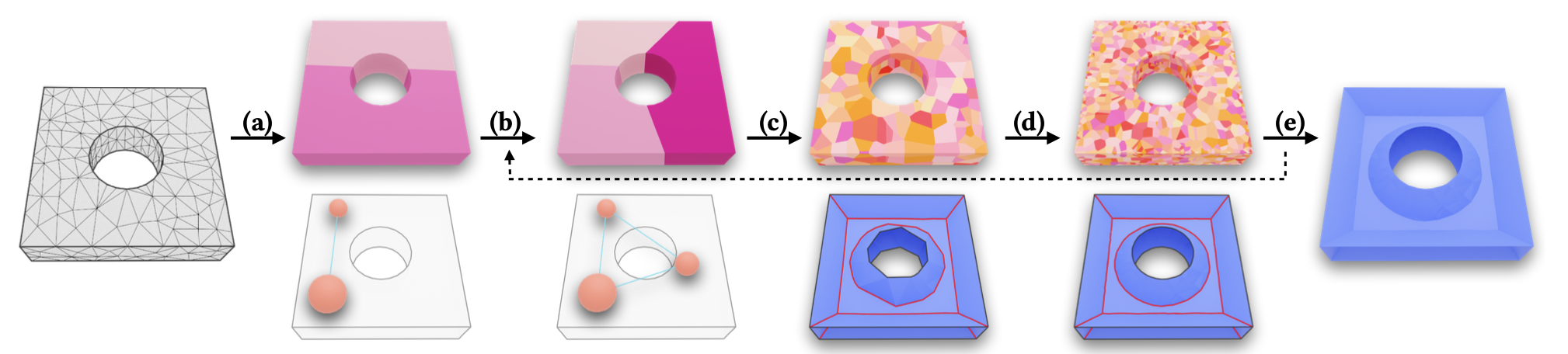
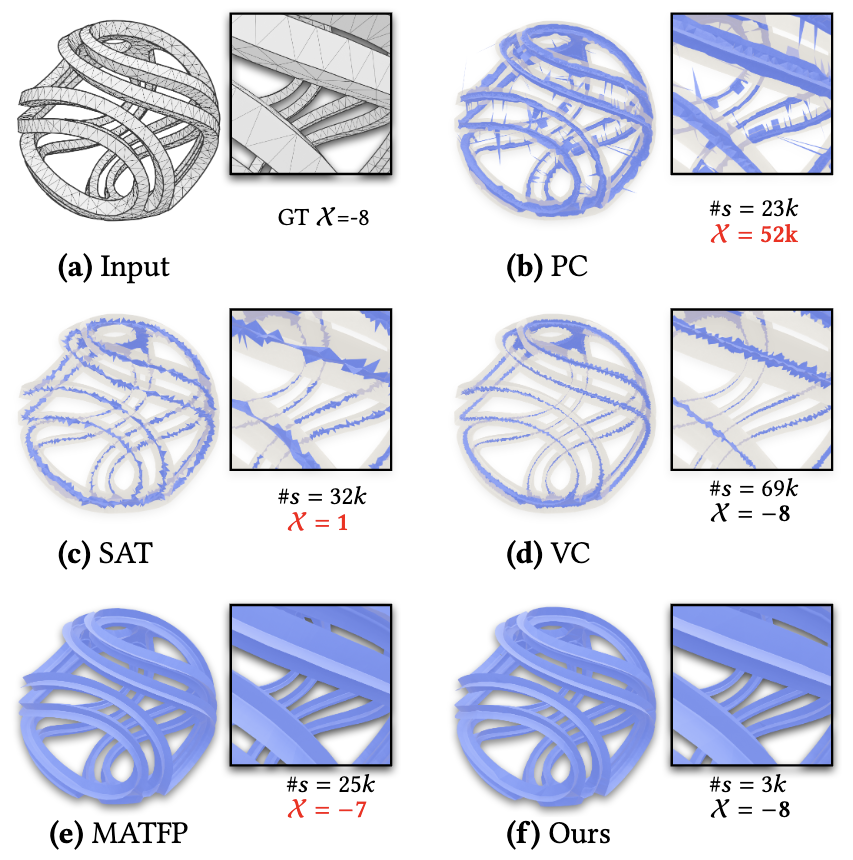
We present a novel topology-preserving 3D medial axis computation framework based on volumetric restricted power diagram (RPD), while preserving the medial features and geometric convergence simultaneously, for both 3D CAD and organic shapes. The volumetric RPD discretizes the input 3D volume into sub-regions given a set of medial spheres. With this intermediate structure, we convert the homotopy equivalency between the generated medial mesh and the input 3D shape into a localized contractibility checking for each restricted element (power cell, power face, power edge), by checking their connected components and Euler characteristics. We further propose a fractional Euler characteristic algorithm for efficient GPU-based computation of Euler characteristic for each restricted element on the fly while computing the volumetric RPD. Compared with existing voxel-based or point-cloud-based methods, our approach is the first to adaptively and directly revise the medial mesh without globally modifying the dependent structure, such as voxel size or sampling density, while preserving its topology and medial features. In comparison with the feature preservation method MATFP, our method provides geometrically comparable results with fewer spheres and more robustly captures the topology of the input 3D shape.

Pipeline

Given a tetrahedral mesh with surface features (sharp edges and corners) pre-detected as input, our method starts with an initial medial mesh of a small number of spheres (i.e., 2 spheres) using the sphere-shrinking algorithm [Ma et al. 2012], shown in (a). Then the homotopy equivalence of the generated medial mesh w.r.t. the input shape is preserved by examining the topological equivalence of individual RPCs (Section 4.1) shown in (b). We preserve the medial features using the same method as MATFP [Wang et al. 2022] (Section 4.2), shown in (c). Finally we preserve the geometric convergence based on a user-defined error threshold (Section 4.3), shown in (d). We repeat this process until both topological preservation and geometric convergence are satisfied, and output the final result of generated medial mesh, shown in (e).

Topological Comparison

Qualitative comparison of topology preservation between our method and MATFP [Wang et al. 2022], PC [Amenta et al. 2001], SAT [Miklos et al. 2010], and VC [Yan et al. 2018]. The ground truth Euler characteristic X is shown in (a), and #𝑠 represents the number of medial spheres generated.

More Results

Visualization of models shown in Table 2, with their model ID and Euler characteristic X. From left to right are the input tetrahedral meshes, the generated medial meshes, the surfaces reconstructed from our medial meshes, and the extracted medial features. For the medial features, the black curves are the external features and the red curves are the internal features.


Citation

@article{wang2024mattopo,
  title     = {MATTopo: Topology-preserving Medial Axis Transform with Restricted Power Diagram},
  author    = {Wang, Ningna and Huang, Hui and Song, Shibo and Wang, Bin and Wang, Wenping and Guo, Xiaohu},
  journal   = {ACM Transactions on Graphics (TOG)},
  year      = {2024},
  address   = {New York, NY, USA},
  publisher = {ACM},
  volume    = {43},
  number    = {4},
  url       = {https://doi.org/10.1145/3687763},
  doi       = {10.1145/3687763},
  booktitle = {ACM SIGGRAPH Asia 2024 Papers},
  series    = {SIGGRAPH Asia '24}
}